Hierarchies in Knowledge Representation

Some Basic Use Cases from KBpedia

Download PDF

The human propensity to categorize is based on trying to make sense of the world. The act of categorization is based on how to group things together and how to relate those things and groups to one another. Categorization demands that we characterize or describe the things of the world using what we have termed attributes in order to find similarities [1]. Categorization may also be based on the relationships of things to external things [2]. No matter the method, the results of these categorizations tend to be hierarchical, reflective of what we see in the natural world. We see hierarchies in Nature based on bigger and more complex things being comprised of simpler things, based on fractals or cellular automata, or based on the evolutionary relationships of lifeforms. According to Annila and Kuismanen, “various evolutionary processes naturally emerge with hierarchical organization” [3]. Hierarchy, and its intimate relationship with categorization and categories, is thus fundamental to the why and how we can represent knowledge for computable means.

Depending on context, we can establish hierarchical relationships between types, classes or sets, with instances or individuals, with characteristics of those individuals, and between all of these concepts. There is potentially different terminology depending on context, and the terminology or syntax may also carry formal understanding of how we can process and compute these relationships. Nillson provides a general overview of these kinds of considerations with a useful set of references [4].

Types of Hierarchical Relationships

As early as 1997 Doyle noted in the first comprehensive study of KR languages, “Hierarchy is an important concept. It allows economy of description, economy of storage and manipulation of descriptions, economy of recognition, efficient planning strategies, and modularity in design.” He also noted that “hierarchy forms the backbone in many existing representation languages” [5].

The basic idea of a hierarchy is that some item (‘thing’) is subsidiary to another item. Categorization, expressed both through the categories themselves and the process of how one splits and grows categories, is a constant theme in knowledge representation. The idea of hierarchy is central to what is treated as a category or other such groupings and how those categories or groupings are tied together. A hierarchical relationship is shown diagrammatically in Figure 1 with A or B, the ‘things’, shown as nodes.

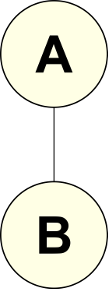
Figure 1: Direct Hierarchy

All this diagram is really saying is that A has some form of superior or superordinate relationship to B (or vice versa, that B is subordinate to A). This is a direct hierarchical relationship, but one of unknown character. Hierarchies can also relate more than two items:

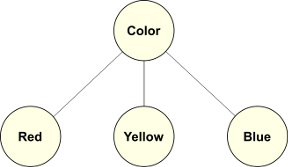
In this case, the labels of the items may seem to indicate the hierarchical relationship, but relying on labels is wrong. For example, let’s take this relationship, where our intent is to show the mixed nature of primary and secondary colors [6]:

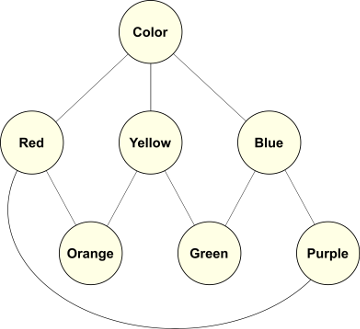
Yet perhaps our intent was rather to provide a category for all colors to be lumped together, as instances of the concept ‘color’ shows here:

Figure 4: Extensional Hierarchy

The point is not to focus on colors – which are, apparently, more complicated to model than first blush – but to understand that hierarchical relations are of many types and what one chooses about a relation carries with it logical implications, the logic determined by the semantics of the representation language chosen and how we represent it. For this clarity we need to explicitly define the nature of the hierarchical relationship. Here are some (vernacular) examples one might encounter:

Table 1: Example Hierarchical Relationships

Again, though we have now labeled the relationships, which in a graph representation are the edges between the nodes, it is still unclear the populations to which these relations may apply and what their exact semantic relationships may be.

Table 2 shows the basic hierarchical relations that one might want to model, and whether the item resides in the universal categories of Charles Sanders Peirce of Firstness, Secondness or Thirdness, introduced in one of my previous articles [7]:

Table 2: Possible Pairwise (―) Hierarchical Relationships

Note that, depending on context, some of the items may reside in either Secondness or Thirdness (depending on whether the referent is a particular instance or a general). Also note the familial relationships shown: child-parent-grandparent and child-child relationships occur in actual families and as a way of talking about inheritance or relatedness relations. The idea of type or is-a is another prominent one in ontologies and knowledge graphs. Natural classes or kinds, for example, fall into the type-token relationship. Also note that mereological relationships, such as part-whole, may also leave open ambiguities. We also see certain pairs, such a sub-super, child-parent, or part-whole, need context to resolve the universal category relation.

Reliance on item labels alone for the edges and nodes, even for something as seemingly straightforward as color or pairwise relationships, does not give us sufficient information to determine how to evaluate the relationship nor how to properly organize. We thus see in knowledge representation that we need to express our relationships explicitly. Labels are merely assigned names that, alone, do not specify the logic to be applied, what populations are affected, or even the exact nature of the relationship. Without these basics, our knowledge graphs can not be computable. Yet well over 95% of the assignments in contemporary knowledge bases have this item-item character. We need interpretable relationships to describe the things that populate our domains of inquiry so as to categorize that world into bite-sized chunks.

Salthe categorizes hierarchies into two types: compositional hierarchies and subsumption hierarchies [8]. Mereological and part-whole hierarchies are compositional, as are entity-attribute. Subsumption hierarchies are ones of broader than, familial, or evolutionary. Cottam et al. believe hierarchies to be so basically important as to propose a model abstraction over all hierarchical types, including levels of abstraction [9]. These discussions of structure and organization are helpful to understand the epistemological bases underlying various kinds of hierarchy. We should also not neglect recursive hierarchies, such as fractals or cellular automata, which are also simple, repeated structures commonly found in Nature. Fortunately, Peirce’s universal categories provide a powerful and consistent basis for us to characterize these variations. When paired with logic and KR languages and “cutting Nature at its joints” [10], we end up with an expressive grammar for capturing all kinds of internal and external relations to other things.

So far we have learned that most relationships in contemporary knowledge bases are of a noun-noun or noun-adjective nature, which I have loosely lumped together as hierarchical relationships. These relationships span from attributes to instances (individuals) and classes [11] or types, with and between one another. We have further seen that labels either for the subjects (nodes) or for their relationships (edges) are an insufficient basis for computers (or us!) to reason over. We need to ground our relationships in specific semantics and logics in order for them to be unambiguous to reasoning machines.

Structures Arising from Hierarchies

Structure needs to be a tangible part of thinking about a new KR installation, since many analytic choices need to be supported by the knowledge artifact. Different kinds of structure are best for different tools or kinds of analysis. The types of relations chosen for the artifact affects its structural aspects. These structures can be as simple and small as a few members in a list, to the entire knowledge graph fully linked to its internal and external knowledge sources. Here are some of the prominent types of structures that may arise from connectedness and characterization hierarchies:

• Lists — unordered members or instances, with or without gaps or duplicates, useful for bulk assignment purposes. Lists generally occur through a direct relation assignment (e.g., rdf:Bag)
• Neural networks (graphs) — graph designs based on connections modeled on biological neurons, still in the earliest stages with respect to relations and KR formalisms [12]
• Ontologies (graphs) — sometimes ontologies are treated as synonymous with knowledge graphs, but more often as a superset that may allow more control and semantic representation [13] Ontologies are a central design feature of KBpedia [14]
• Parts-of-speech — a properly designed ontology has the potential to organize the vocabulary of the KR language itself into corresponding parts-of-speech, which greatly aids natural language processing
• Sequences — ordered members or instances, with or without gaps or duplicates, useful for bulk assignment purposes. Sequences generally occur through a direct relation assignment (e.g., rdf:Seq)
• Taxonomies (trees)— trees are subsumption hierarchies with single (instances may be assigned to only one class) or multiple (instances may be assigned to multiple classes or types) inheritance. The latter is the common scaffolding for most knowledge graphs
• Typologies — are essentially multi-inheritance taxonomies, with the hierarchical organization of types as natural as possible. Natural types (classes or kinds) enable the greatest number of disjoint assertions to be made, leading to efficient processing and modular design. Typologies are a central design feature of KBpedia; see further [15].

Typically KR formalisms and their internal ontologies (taxonomy or graph structures) have a starting node or root, often called ‘thing’, ‘entity’ or the like. Close inspection of the choice of root may offer important insights. ‘Entity’, for example, is not compatible with a Peircean interpretation, since all entities are within Secondness.

KBpedia’s foundational structure is the subsumption hierarchy shown in the KBpedia Knowledge Ontology (KKO) — that is, KBpedia’s upper ontology — and its nodes derived from the universal categories. The terminal, or leaf, nodes in KKO each tie into typologies. All of the typologies are themselves composed of types, which are the hierarchical classification of natural kinds of instances as determined by shared attributes (though not necessarily the same values for those attributes). Most of the types in KBpedia are composed of entities, but attributes and relations also have aggregations of types.

Of course, choice of a KR formalism and what structures it allows must serve many purposes. Knowledge extension and maintenance, record design, querying, reasoning, graph analysis, logic and consistency tests, planning, hypothesis generation, question and answering, and subset selections for external analysis are properly the purview of the KR formalism and its knowledge graph. Yet other tasks such as machine learning, natural language processing, data wrangling, statistical and probabalistic analysis, search indexes, and other data- and algorithm-intensive applications are often best supported by dedicated external applications. The structures to support these kinds of applications, or the ability to export them, must be built into the KR installation, with explicit consideration for the data forms and streams useful to possible third-party applications.